遗传算法聚类程序
本文内容遵从CC版权协议, 可以随意转载, 但必须以超链接形式标明文章原始出处和作者信息及版权声明网址: http://www.penglixun.com/tech/ai/genetic_algorithm_clustering.html
何为遗传算法,概念性的描述我就不说了,摘自维基百科:
遗传算法是计算数学中用于解决最优化的搜索算法,是进化算法的一种。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的,这些现象包括遗传、突变、自然选择以及杂交等。
遗传算法通常实现为一种计算机模拟。对于一个最优化问题,一定数量的候选解(称为个体)的抽象表示(称为染色体)的种群向更好的解进化。传统上,解用二进制表示(即0和1的串),但也可以用其他表示方法。进化从完全随机个体的种群开始,之后一代一代发生。在每一代中,整个种群的适应度被评价,从当前种群中随机地选择多个个体(基于它们的适应度),通过自然选择和突变产生新的生命种群,该种群在算法的下一次迭代中成为当前种群。
我来描述下我的问题,需要从数百万个5维点中选出32个聚类中心(可以不是原集合中的点),将点全部按就近原则聚类到这个三十二个区域,要求最终所有点到自己聚类中心的点最短。
初看这个问题,很多人会采用K-均值算法,不过我觉得这个问题用遗传算法做正好。
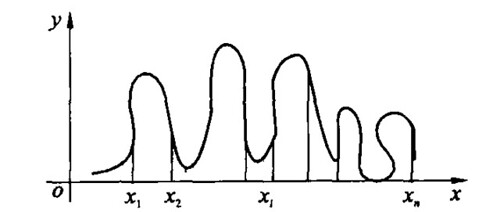
遗传算法实际上就像是在图中的曲线上放了个小球,小球会滚向我们所选区间的最低谷,如果选的区间大,运算量就大,但是不容易错过最低点,极限就是区间是全部X轴,这就成枚举了。而区间适当放大,在区间内滚动,然后随着滚动校正区间,可能就会获得最优解。但是也可能所选的区间不够大,小球落在极小点,而不是最小点。
可能描述有点混乱,请谅解,我文字描述能力实在是不强……
我解决这个问题的思路是,将32个点当做一条“染色体”,初始化随机100个“染色体”,计算适应度(每个点选择一个最近点,把距离加到总和)。
得到适应度后,为了保存优秀“基因”,我采取了“精英保留法”,每代选择最佳适应度的4个“精英”抽中其中一个直接进入下轮进化,而不参与变异,这样可以保证最接近结果的“染色体”被保留,又可以避免极小点被一直保留。
剩下的“染色体”每次随机选取两个,根据杂交率参数控制是否进行“杂交”,如果进行“杂交”,互换一部分DNA(中心点),得到新的“染色体”。
然后对新的“染色体”根据变异率参数控制是否进行“变异”,如果进行“变异”操作,则对“染色体”中的DNA随机根据最大干扰度参数改变值(就是对点的维度坐标稍微修正)。
最后为了程序不一直无限执行下去,设定最大遗传代数,来控制到了最大代数则停止,输出结果。
我的程序中Dat.txt是一部分测试数据,我转换成了二进制,在Dat.bin中,程序为了速度实际是读取Dat.bin中的数据。最后结果输出在Best.txt,包含选中的32个聚类中心,Res.txt包含了程序执行的全过程,包括每代的进化情况和适应度变化。
参数在Params.ini都可以修改,含义见“说明.txt”。
想测试准备好一下午,测试数据有十几万个点,可以算两到四个小时,算法还有优化的余地……
 GenAlg.7z (4.2 MiB, 1,758 hits)
GenAlg.7z (4.2 MiB, 1,758 hits)
运算过程输出如下:(每组点实际上就是一个“染色体”,每个点就是一个DNA)
—–第163代—–
**最短距离:1962.894220127**
**最长距离:1962.899054822**
第1组点:
适应度:1.000000000
#第1点#:0.030828948 0.072564733 0.106285252 0.051868469 0.172346768
#第2点#:0.026975404 0.071053079 0.037076164 0.015429519 0.235267262
#第3点#:0.021837669 0.074076457 0.097634142 0.064353437 0.183289753
#第4点#:0.019589556 0.077099688 0.034604356 0.013544861 0.166875506
#第5点#:0.011561215 0.075588291 0.063029879 0.026044048 0.210646204
#第6点#:0.020231740 0.071052930 0.028425015 0.016265740 0.350165005
#第7点#:0.003532547 0.077099741 0.001235945 0.000026277 0.131311960
#第8点#:0.002247871 0.072564576 0.000000208 0.000000279 0.172346749
#第9点#:0.011882187 0.075588419 0.046963139 0.020063039 0.169610949
#第10点#:0.001926884 0.074076575 0.000000035 0.000300025 0.254417049
#第11点#:0.002890176 0.071053149 0.003707985 0.002017947 0.186025315
#第12点#:0.020231665 0.074076658 0.040783984 0.013612235 0.150461535
#第13点#:0.019268258 0.074076374 0.011122899 0.004418380 0.202439243
#第14点#:0.021195254 0.075588085 0.025953226 0.015328270 0.309130186
#第15点#:0.001605883 0.075588242 0.008651180 0.004358942 0.166875224
#第16点#:0.024085315 0.068029402 0.007415315 0.001622046 0.128576210
#第17点#:0.014451387 0.072564782 0.027189252 0.010447178 0.191496596
#第18点#:0.009313056 0.065006161 0.000000261 0.000389068 0.103954996
#第19点#:0.015414793 0.077100085 0.064265239 0.030003327 0.194232027
#第20点#:0.003211451 0.068029729 0.001235622 0.000558517 0.213381682
#第21点#:0.007064990 0.074076404 0.023481607 0.015341144 0.205174976
#第22点#:0.003532473 0.074076569 0.004943461 0.003667342 0.227060020
#第23点#:0.015414787 0.071052886 0.049434890 0.020560016 0.188760866
#第24点#:0.028902382 0.068029598 0.046963399 0.033677853 0.232531453
#第25点#:0.001284925 0.071052977 0.000000122 0.002158284 0.391200344
#第26点#:0.027617828 0.069541116 0.087746906 0.021012635 0.191496221
#第27点#:0.016699051 0.074076470 0.082803520 0.027715665 0.153197049
#第28点#:0.013166553 0.072564636 0.016066286 0.004394788 0.150461344
#第29点#:0.014772403 0.072564532 0.025953453 0.006279025 0.224324775
#第30点#:0.013166404 0.049888089 0.019773628 0.006398813 0.218853029
#第31点#:0.008028441 0.057446823 0.008650953 0.002620522 0.164139773
#第32点#:0.002890405 0.065005962 0.002471714 0.001722612 0.254417026
第2组点:
适应度:1.000039299
#第1点#:0.030828948 0.072564733 0.106285252 0.051868469 0.172346768
#第2点#:0.026975404 0.071053079 0.037076164 0.015429519 0.235267262
#第3点#:0.021837669 0.074076457 0.097634142 0.064353437 0.183289753
#第4点#:0.019589556 0.077099688 0.034604356 0.013544861 0.166875506
#第5点#:0.011561215 0.075588291 0.063029879 0.026044048 0.210646204
#第6点#:0.020231685 0.071052937 0.028425017 0.016265727 0.350164999
#第7点#:0.003532545 0.077099704 0.001235963 0.000026254 0.131311950
#第8点#:0.002247871 0.072564576 0.000000208 0.000000279 0.172346749
#第9点#:0.011882187 0.075588419 0.046963139 0.020063039 0.169610949
#第10点#:0.001926884 0.074076575 0.000000035 0.000300025 0.254417049
#第11点#:0.002890176 0.071053149 0.003707985 0.002017947 0.186025315
#第12点#:0.020231665 0.074076658 0.040783984 0.013612235 0.150461535
#第13点#:0.019268258 0.074076374 0.011122899 0.004418380 0.202439243
#第14点#:0.021195254 0.075588085 0.025953226 0.015328270 0.309130186
#第15点#:0.001605883 0.075588242 0.008651180 0.004358942 0.166875224
#第16点#:0.024085315 0.068029402 0.007415315 0.001622046 0.128576210
#第17点#:0.014451405 0.072564838 0.027189179 0.010447134 0.191496561
#第18点#:0.009313116 0.065006211 0.000000224 0.000389070 0.103955071
#第19点#:0.015414793 0.077100085 0.064265239 0.030003327 0.194232027
#第20点#:0.003211451 0.068029729 0.001235622 0.000558517 0.213381682
#第21点#:0.007064990 0.074076404 0.023481607 0.015341144 0.205174976
#第22点#:0.003532473 0.074076569 0.004943461 0.003667342 0.227060020
#第23点#:0.015414851 0.071052899 0.049434867 0.020559980 0.188760858
#第24点#:0.028902382 0.068029598 0.046963399 0.033677853 0.232531453
#第25点#:0.001284925 0.071052977 0.000000122 0.002158284 0.391200344
#第26点#:0.027617764 0.069541111 0.087746863 0.021012623 0.191496151
#第27点#:0.016699051 0.074076470 0.082803520 0.027715665 0.153197049
#第28点#:0.013166632 0.072564581 0.016066295 0.004394711 0.150461374
#第29点#:0.014772403 0.072564532 0.025953453 0.006279025 0.224324775
#第30点#:0.013166404 0.049888089 0.019773628 0.006398813 0.218853029
#第31点#:0.008028441 0.057446823 0.008650953 0.002620522 0.164139773
#第32点#:0.002890405 0.065005962 0.002471714 0.001722612 0.254417026

我。。果然只能路过。。。顺带膜拜。。
请问下 适应度函数具体是怎么执行的 谢谢!